Classification of soil
Types of soil (on the basis of moisture content)
Saturated
A saturated soil is a two phase material consisting of a soil skeleton and voids which are saturated with water. It is reasonable to expect that the behavior of an element of such a material will be influenced not only by the forces applied to its surface but also by the water pressure of the fluid in the pores. Suppose that a soil sample having a uniform cross sectional area A is subjected to an applied load W, then it is found that the soil will deform. If however, the sample is loaded by increasing the height of water in the containing vessel, as shown in Fig lb, then no deformation occurs.
A saturated soil is a two phase material consisting of a soil skeleton and voids which are saturated with water. It is reasonable to expect that the behavior of an element of such a material will be influenced not only by the forces applied to its surface but also by the water pressure of the fluid in the pores. Suppose that a soil sample having a uniform cross sectional area A is subjected to an applied load W, then it is found that the soil will deform. If however, the sample is loaded by increasing the height of water in the containing vessel, as shown in Fig lb, then no deformation occurs.
|
- Coarse
- Fine
- Organic
- Gravel
- Sand
- Clay
- Silt
- Boulders
- Cobbles
- Peat
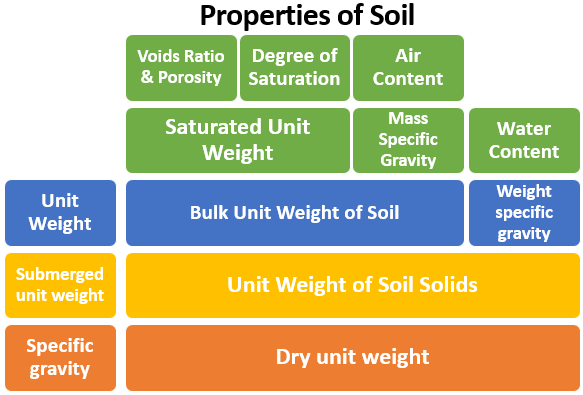
Soil Properties
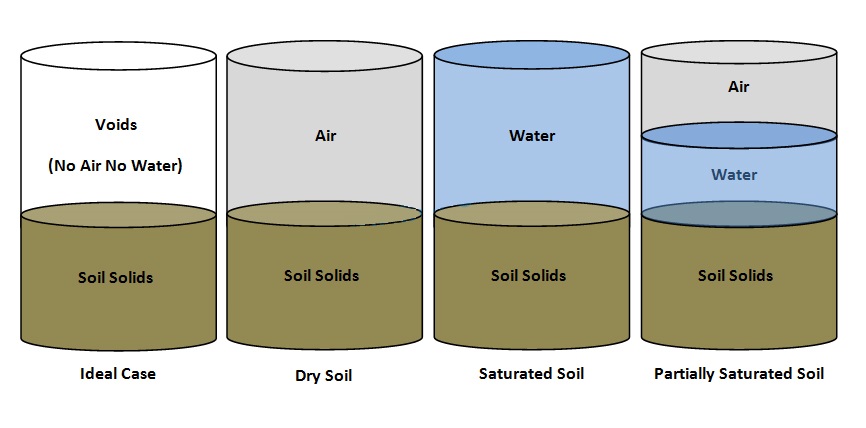
- Soil Particles with NO AIR and NO WATER in voids (Ideal Case i.e. 100% Compacted Soil)
- Soil Particles with ONLY AIR in voids (Dry Soil)
- Soil Particles with ONLY WATER in voids (Saturated Soil)
- Soil Particles with BOTH AIR and WATER in voids (Partially Saturated Soil)
Gravel
|
Sand
|
Silt
|
Clay
| ||||||||
Coarse
|
Medium
|
Fine
|
Coarse
|
Medium
|
Fine
|
Coarse
|
Medium
|
Fine
|
Coarse
|
Medium
|
Fine
|
60
|
20
|
6
|
2
|
0.6
|
0.2
|
0.06
|
0.02
|
0.006
|
0.002
|
0.0006
|
0.0002
|
Table 1. Particle Size Boundaries
Using volumes is not very convenient in most calculations. An alternative measure that is used is the voids ratio, e. This is defined as the ratio of the volume of voids, Vv to the volume of solids, Vs, that is A related quantity is the porosity, n, which is defined as ratio of the volume of voids to the total volume.
Mathematically
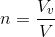
Porosity
It is defined as “The ratio of the volume of voids to the total volume of soil sample". It is denoted by “n”
Mathematically
Porosity = (Volume of Voids/Volume of Soil Sample)
2. Degree of Saturation
It is the ratio of the Volume of Water to the Volume of Voids. It is denoted by “S”
Mathematically
Degree of Saturation = (Volume of Water / Volume Voids)
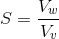
It is expressed in percentage and is also known as Percent Saturation. In a fully saturated sample;
Vw = Vv
Hence S = 1 or 100%
In case of dry sample Vw = 0, thus
S = 0
The degree of saturation, S, has an important influence on the soil behavior. It is defined as the ratio of the volume of water to the volume of voids.
3. Air content:
It is the ratio of Volume of Air to the Volume of Voids present in the given soil sample
Mathematically
Air Content = (Volume of Air/Volume of Voids)
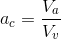
Void Ratio, Porosity, Degree of Saturation and Air Content are Volume Ratio.
4. Water content:
It is defined as “The ratio of the weight of water to the weight of solids”
Mathematically
Water Content =(Weight of Water /Weight of Solids)
It is denoted by w
As a single quantity it is expressed in percentage. In Relationships or Formulae, it is expressed in fraction .
The moisture content, m, is a very useful quantity because it is simple to measure. It is defined as the ratio of the weight of water to the weight of solid material. The water content (also known as moisture content) test is probably the most common and simplest type of laboratory test. This test can be performed on disturbed or undisturbed soil specimens.
The water content test consists of determining the mass of the wet soil specimen and then drying the soil in an oven overnight (12 to 16 hr) at a temperature of 110 °C (ASTM D 2216-92, 1998). The water content (w) of a soil is defined as the mass of water in the soil (Mw) divided by the dry mass of the soil (Ms), expressed as a percentage (i.e., w _ 100 Mw/Ms). Values of water content (w) can vary from essentially 0% up to 1200%. A water content of 0% indicates a dry soil. An example of a dry soil would be near-surface rubble, gravel, or clean sand located in a hot and dry climate. Soil having the highest water content is organic soil, such as fibrous peat, which has been reported to have water content as high as 1200%.
The water content test consists of determining the mass of the wet soil specimen and then drying the soil in an oven overnight (12 to 16 hr) at a temperature of 110 °C (ASTM D 2216-92, 1998). The water content (w) of a soil is defined as the mass of water in the soil (Mw) divided by the dry mass of the soil (Ms), expressed as a percentage (i.e., w _ 100 Mw/Ms). Values of water content (w) can vary from essentially 0% up to 1200%. A water content of 0% indicates a dry soil. An example of a dry soil would be near-surface rubble, gravel, or clean sand located in a hot and dry climate. Soil having the highest water content is organic soil, such as fibrous peat, which has been reported to have water content as high as 1200%.
5. Unit weight:
Several unit weights are used in Soil Mechanics. These are the bulk, saturated, dry, and submerged unit weights. The bulk unit weight is simply defined as the weight per unit volume. It is defined as “the weight of soil per unit volume of soil”.
Mathematically
Unit Weight of Soil= (Weight of Soil /Volume of Soil)
It is denoted by “ γ ”
It is expressed in 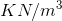
6. Bulk Unit Weight of Soil:
It is sometimes called Unit Weight only. It is the ratio of the total weight of soil to the total volume of soil.
Mathematically
Bulk Unit Weight of Soil = (Weight of Soil/ Total Volume of Soil)
It is also called Moist Unit Weight. The weight of the aggregate that fills a 1-cubic-foot container. This term is used because the volume contains both aggregate and voids air spaces.
The total unit weight (also known as the wet unit weight) should only be obtained from undisturbed soil specimens, such as those extruded from Shelby tubes or on undisturbed block samples obtained from test pits and trenches. The first step in the laboratory testing is to determine the wet density, defined as _t _ M/V, where M _ total mass of the soil, which is the sum of the mass of water (Mw) and mass of solids (Ms), and V _ total volume of the soil
7. Unit Weight of Soil Solids
It is defined as “the weight of soil solid per unit total volume of soil solid”
Mathematically
Unit Weight of Soil Solid = ( Weight of Soil Solids/Volume of Soil)
8. Dry unit weight
It is defined as “ the weight of soil solids per unit total volume of sample”
Mathematically
Dry Unit Weight of Soil = ( Weight of Soil Solids/Total Volume of Soil)
Since
W = Wa + Ww + Ws = 0 + 0 + Ws = Ws = Wd , therefore,
When all the voids of soil are filled with air it is called Dry Soil and Unit Weight as Dry Unit Weight e.g. Oven Dried Soil in Laboratory
9. Saturated unit weight
It is defined as “the total weight of saturated soil sample per units its total volume”
Mathematically
When all the voids of soil are filled with water it is called Saturated Soil and its weight as Saturated Unit Weight
10. Submerged unit weight
It is defined as “the submerge weight of soil per unit its total volume”
Mathematically
Submerged Unit Weight = (Submerged Weight of Soil/ Total Volume of Soil)
According to the Archimedes’ Principle;
An object immersed in water will experience a buoyant force in upward direction causing reduction in weight. Thus soil submerged in water will thus have a unit weight.
11. Specific gravity:
It is defined as “the ratio of the unit weight of soil sample to the unit weight of water at standard temperature and pressure i.e. 4°C and 1 atm or 101.325 kPa
OR
It is defined as “the ratio of the density of soil sample to the density of water at standard temperature and pressure i.e. 4°C and 1 atm or 101.325 kPa
Mathematically
Specific Gravity = (Unit weight of Soil/Unit Weight of Water)
It is denoted by G or S.G.
The specific gravity (G) is a dimensionless parameter that is defined as the density of solids (_s) divided by the density of water (_w), or G _ _s / _w. The density of solids (_s) is defined as the mass of solids (Ms) divided by the volume of solids (Vs). The density of water (_w) is equal to 1 g/cm3 (or 1 Mg/m3) and 62.4 pcf. For soil, the specific gravity is obtained by measuring the dry mass of the soil and then using a pycnometer to obtain the volume of the soil.
Because quartz is the most abundant type of soil mineral, the specific gravity for inorganic soil is often assumed to be 2.65. For clays, the specific gravity is often assumed to be 2.70 because common clay particles, such as montmorillonite and illite, have slightly higher specific gravity value.
12. Mass specific gravity
13. Weight specific gravity
Three Phase System of Soil
A soil mass is a three phase system consisting of solid particles (soil grains), water and air. Thus four cases arises

 pile driving equipment consists of a heavy ram in between the leads. The ram is lifted up to a certain height and released to drop on the pile. This type is slow and therefore not in common use. It is used in the cases where only a small number of piles are driven.
pile driving equipment consists of a heavy ram in between the leads. The ram is lifted up to a certain height and released to drop on the pile. This type is slow and therefore not in common use. It is used in the cases where only a small number of piles are driven.

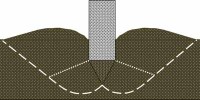 Failure pattern consists of wedge and slip surface but is well defined only under the footing. Slight bulging of soil surface occurs. Tilting of footing is not expected.
Failure pattern consists of wedge and slip surface but is well defined only under the footing. Slight bulging of soil surface occurs. Tilting of footing is not expected.